وظيف تحويل العبارة في حل بعض النماذج من المعادلات المثلثية :

سنقتصر دراستنا على حل النماذج الآتية من المعادلات

 1)     

  2)

             حيث a , b  ليسا صفرين معاً , ؤ c ليس صفرا

    3)  

  النموذج الاول :

 مثال : حل المعادلة :

حيث أن  

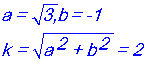   نقسم المعادلة على 2 فنجد

ومنه

ولهذه المعادلة حلان

الحل الاول :  

  ومنه

الحل الثاني : ومنه

 الشرط الازم والكافي لقابلية المعادلة للحل هو

  ومن المعلوم يبقى صحيحا في حالة

وكذلك

مثال : ابحث عن حلول المعادلة :

ااذن لمعادلة مستحلية     

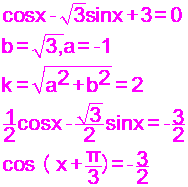
مثال (3):عين L من R (مجموعة الاعداد الحقيقية)التي تجعل المعادلة

قابلة حل ثم اوجد حلها عندما     

الحل :شرط الحل

نعوض في المعادلة المفروضة  لكن عندما   

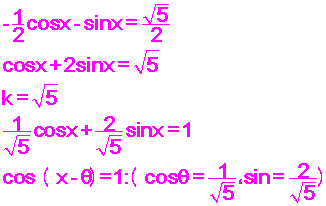
ومجموعة حلولها

النموذج الثاني  

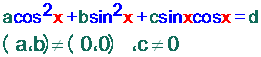
يرد هذا النموذج الى النموذج الاول باستخدام العلاقات

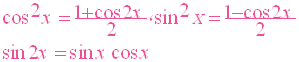
مثال

حل المعادلة

الحل

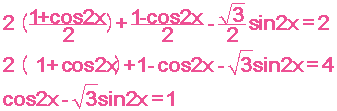
وهي معادلة من النموذج الأول تحول الى الشكل

 لهذه المعادلة حلان

              الاول

    الثاني 

النموذج الثالث

مثال

حل المعادلة

 فنجدcosx+sinx  الحل نحول العبارة

 نعوض في المعادلة    نفرض

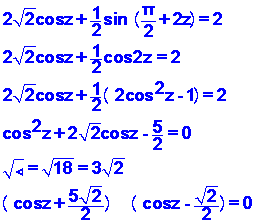
 لاينعدم  وبما أن

فان

ولهذه المعادلة حلان

الحل الاول

الحل الثاني

(تمرينات (1

1)حل في R المعادلات الآتية :

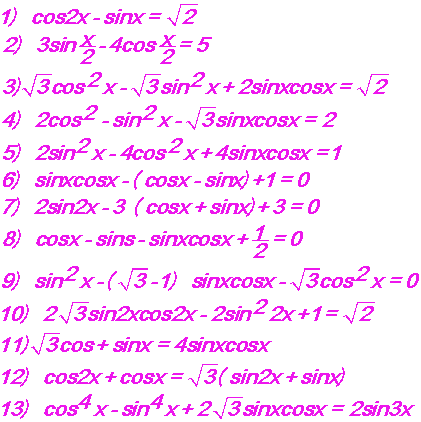
 الأمثلة محلولة

النموذج الأول:

مثال : حل المعادلة

الحل :  نقسم حدود المعادلة على 2 فنجد :

هذه المعادلة بسيطة لها حلان :

                                  وهو المطلوب

مثال:  لدينا المعادلة  المطلوب

1)   عين قيم التي تجعل للمعادلة حل في

2)    بفرض 1=حل هذه المعادلة

الحل : شرط حل المعادلة       هو

لحل هذه المتراجحة : مستحلة الحل في   إذن اشارة

 توافق إشارة أمثال  موجبة تماماً إذن

2) عندما  نبدل    نموذج الأول تحويل العبارة نقسم على 

هذه المعادلة بسيطة لها حلان :

اما   أو 

النموذج الثاني

مثال :  حل المعادلة :

وهي معادلة من النموذج الأول : تحول إلى الشكل  لهذه المعادلة حلان

وهو المطلوب

النموذج الثالث

مثال : حل المعادلة :

الحل : نحول العبارة :  فنجد :    نفرض  عندئذ

  نعوض في المعادلة :

بما أن    لا ينعدم فإن  

 ولهذه المعادلة حلان

تمرينات

حل في R المعادلات التالية